Somme de trois cubes

En mathématiques, le problème de la somme de trois cubes est un problème non résolu en théorie des nombres. Il consiste à déterminer quels sont les entiers ${\displaystyle n\in \mathbb {Z} }$ qui peuvent être représentés sous la forme d'une somme de trois cubes d'entiers ${\displaystyle x^{3},y^{3},z^{3}\in \mathbb {Z} }$, donc qui peuvent s'écrire sous la forme : ${\displaystyle x^{3}+y^{3}+z^{3}=n}$ avec ${\displaystyle x,y,z\in \mathbb {Z} }$.

Exemples

Voici quelques exemples :

${\displaystyle 3=1^{3}+1^{3}+1^{3}}$

${\displaystyle 10=1+1+8=1^{3}+1^{3}+2^{3}}$

${\displaystyle 36=1+8+27}$

${\displaystyle 20=1+(-8)+27=1^{3}+(-2)^{3}+3^{3}}$

et un exemple plus compliqué :

${\displaystyle 16=(-511)^{3}+(-1609)^{3}+1626^{3}.}$

Les suites de l'OEIS :  A060465,  A060466,  A060467 donnent respectivement les valeurs de ${\displaystyle x,y,z}$ pour ${\displaystyle x^{3}+y^{3}+z^{3}=n}$ où ${\displaystyle n}$ est un entier naturel congru ni à 4 ni 5 modulo 9, avec ${\displaystyle |y|,|z|}$ minimaux et ${\displaystyle |x|\leqslant |y|\leqslant |z|}$.

Petites valeurs de n

On peut montrer qu'une condition nécessaire pour que ${\displaystyle n}$ s'exprime comme somme de trois cubes est que ${\displaystyle n}$ n'est pas congru à 4 ou 5 modulo 9, car les cubes sont égaux à 0, 1, ou −1 modulo 9, et la somme de trois de ces nombres ne donne ni 4 ni 5 modulo 9. On ne sait pas si cette condition nécessaire est aussi suffisante.

Une représentation non triviale de ${\displaystyle n=0}$ comme somme de trois cubes serait un contre-exemple au dernier théorème de Fermat pour l'exposant 3, car l'équation ${\displaystyle x^{3}+y^{3}+z^{3}=0}$ se réécrit ${\displaystyle x^{3}+y^{3}=z'^{3}}$ avec ${\displaystyle z'=-z}$, et comme l'a déjà prouvé Leonhard Euler, les seules solutions ont la forme

${\displaystyle a^{3}+(-a)^{3}+0^{3}=0}$.

Pour la représentation de ${\displaystyle n=1}$ et ${\displaystyle n=2}$, il existe une infinité de solutions

${\displaystyle (9b^{4})^{3}+(3b-9b^{4})^{3}+(1-9b^{3})^{3}=1}$ découverte par Kurt Mahler en 1936

et

${\displaystyle (1+6c^{3})^{3}+(1-6c^{3})^{3}+(-6c^{2})^{3}=2.}$ découverte par A. S. Verebrusov en 1908, cité par Louis J. Mordell.

Ces représentations peuvent être modifiées pour donner des représentations d'entiers qui sont des cubes ou les doubles d'un cube. D'autres représentations, et d'autres familles paramétrées de représentations existent pour ${\displaystyle n=1}$. Pour ${\displaystyle n=2}$, les autres représentations connues sont^,:

${\displaystyle 1\ 214\ 928^{3}+3\ 480\ 205^{3}+(-3\ 528\ 875)^{3}=2,}$

${\displaystyle 37\ 404\ 275\ 617^{3}+(-25\ 282\ 289\ 375)^{3}+(-33\ 071\ 554\ 596)^{3}=2,}$

${\displaystyle 3\ 737\ 830\ 626\ 090^{3}+1\ 490\ 220\ 318\ 001^{3}+(-3\ 815\ 176\ 160\ 999)^{3}=2.}$

Seules les représentations de 1 et 2 peuvent être paramétrées ainsi par des polynômes de degré 4. Même pour les représentations de 3, Louis J. Mordell écrit en 1953 : « je n'en connais pas d'autres » à propos de ses petites solutions

${\displaystyle 1^{3}+1^{3}+1^{3}=4^{3}+4^{3}+(-5)^{3}=3}$,

et il mentionne qu'en plus, dans ce cas, les trois nombres élevés au cube doivent être égaux modulo 9^,.

Exploration numérique

Depuis 1955 et les études de Mordell, de nombreux auteurs ont cherché des solutions par exploration numérique ^{,,,,,, ,,,}. En 2009, Elsenhans et Jahnel utilisent une méthode de Noam Elkies qui fait usage d'algorithmes de réduction de réseaux pour chercher toutes les solutions de l'équation diophantienne

${\displaystyle x^{3}+y^{3}+z^{3}=n}$

pour des entiers ${\displaystyle n}$ positifs inférieurs à 1000 et pour ${\displaystyle \max(|x|,|y|,|z|)<10^{14}}$, et ils laissent ouvert les valeurs de ${\displaystyle n}$ égales à 33, 42, 74, 114, 165, 390, 579, 627, 633, 732, 795, 906, 921 et 975 parmi les entiers ${\displaystyle n\leq 1000}$. Après une vidéo de Timothy Browning dans Numberphile, Huisman en 2016 étend cette recherche à ${\displaystyle \max(|x|,|y|,|z|)<10^{15}}$ ce qui lui permet de résoudre le cas 74 :

${\displaystyle 74=(-284\ 650\ 292\ 555\ 885)^{3}+66\ 229\ 832\ 190\ 556^{3}+283\ 450\ 105\ 697\ 727^{3}}$.

Grâce ces recherches exhaustives, tous les entiers ${\displaystyle n<100}$ qui ne sont pas congrus à 4 ou 5 modulo 9 possèdent une solution, laissant encore ouvert, à ce stade, les cas 33 et 42.

En mars 2019, Andrew Booker (en) résout le cas ${\displaystyle n=33}$, en découvrant que

${\displaystyle 33=8\ 866\ 128\ 975\ 287\ 528^{3}+(-8\ 778\ 405\ 442\ 862\ 239)^{3}+(-2\ 736\ 111\ 468\ 807\ 040)^{3}}$.

Pour obtenir ce résultat, Booker utilise une autre stratégie de recherche dont le temps de calcul est proportionnel à ${\displaystyle \min(|x|,|y|,|z|)}$ plutôt qu'à leur maximum^,, une approche qui avait déjà été suggérée par Heath-Brown et al.^,. Il a aussi trouvé la représentation

${\displaystyle 795=(-14\ 219\ 049\ 725\ 358\ 227)^{3}+14\ 197\ 965\ 759\ 741\ 571^{3}+2\ 337\ 348\ 783\ 323\ 923^{3},}$

et vérifié qu'il n'y a pas de solutions pour ${\displaystyle n=42}$ et pour tout autre entier ${\displaystyle n\leq 1000}$ de statut inconnu avec ${\displaystyle |z|\leq 10^{16}}$. En septembre 2019, Andrew Booker et Andrew Sutherland (en) résolvent le cas ${\displaystyle n=42}$ et trouvent que

${\displaystyle 42=(-80\ 538\ 738\ 812\ 075\ 974)^{3}+80\ 435\ 758\ 145\ 817\ 515^{3}+12\ 602\ 123\ 297\ 335\ 631^{3}}$.

Ils utilisent pour cela la Charity Engine, un réseau mondial qui exploite la puissance de calcul inutilisée de 500 000 ordinateurs personnels ; le calcul a pris globalement 1,3 million d'heures de calcul. Ils trouvent aussi que

${\displaystyle 906=(-74\ 924\ 259\ 395\ 610\ 397)^{3}+72\ 054\ 089\ 679\ 353\ 378^{3}+35\ 961\ 979\ 615\ 356\ 503^{3}}$

et

${\displaystyle 165=(-385\ 495\ 523\ 231\ 271\ 884)^{3}+383\ 344\ 975\ 542\ 639\ 445^{3}+98\ 422\ 560\ 467\ 622\ 814^{3}\ }$.

Booker et Sutherland ont également trouvé une troisième représentation de ${\displaystyle n=3}$ après encore l'équivalent de 4 millions d'heures d'ordinateur sur Charity Engine, à savoir :

${\displaystyle 3=569\ 936\ 821\ 221\ 962\ 380\ 720^{3}+(-569\ 936\ 821\ 113\ 563\ 493\ 509)^{3}+(-472\ 715\ 493\ 453\ 327\ 032)^{3}.}$^,,.

Cette découverte résout la question posée il y a 65 ans par Louis J. Mordell qui a suscité tant de recherches.

Les cas non résolus jusqu'à 1000 sont désormais 114, 390, 579, 627, 633, 732, 921 et 975.

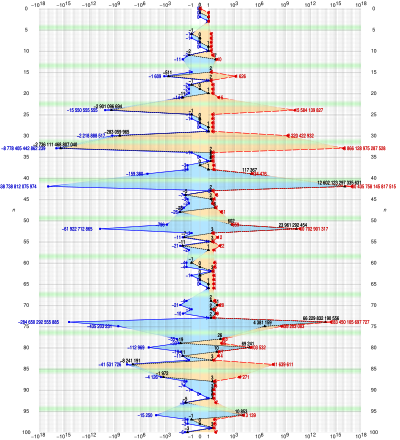
Les entiers ${\displaystyle n\not \equiv 4{\pmod {9}}}$ et ${\displaystyle n\not \equiv 5{\pmod {9}}}$ inférieurs à 100 sont : 0, 1, 2, 3, 6, 7, 8, 9, 10, 11, 12, 15, 16, 17, 18, 19, 20, 21, 24, 25, 26, 27, 28, 29, 30, 33, 34, 35, 36, 37, 38, 39, ... (suite A060464 de l'OEIS) Ci-dessous sont listées les valeurs des solutions ${\displaystyle x}$, ${\displaystyle y}$ et ${\displaystyle z}$ correspondantes de l'équation ${\displaystyle x^{3}+y^{3}+z^{3}=n}$ avec la valeur minimale de ${\displaystyle |y|}$ et ${\displaystyle |z|}$ et ${\displaystyle 0\leq |x|\leq |y|\leq |z|}$:

${\displaystyle x:\quad }$ 0, 0, 0, 1, -1, 0, 0, 0, 1, -2, 7, -1, -511, 1, -1, 0, 1, -11, -2901096694, -1, 0, 0, 0, 1, -283059965, -2736111468807040, -1, 0, 1, 0, 1, 117367, ... (suite A060465 de l'OEIS)

${\displaystyle y:\quad }$ 0, 0, 1, 1, -1, -1, 0, 1, 1, -2, 10, 2, -1609, 2, -2, -2, -2, -14, -15550555555, -1, -1, 0, 1, 1, -2218888517, -8778405442862239, 2, 2, 2, -3, -3, 134476,… (suite A060466 de l'OEIS)

${\displaystyle z:\quad }$ 0, 1, 1, 1, 2, 2, 2, 2, 2, 3, -11, 2, 1626, 2, 3, 3, 3, 16, 15584139827, 3, 3, 3, 3, 3, 2220422932, 8866128975287528, 3, 3, 3, 4, 4, -159380,… ( suite A060467 de l'OEIS )

Dans les quatre listes ci-dessus, la 19^e valeur, est en gras : elles indiquent que pour ${\displaystyle n=24}$ la solution entière la plus petite de l'équation ${\displaystyle x^{3}+y^{3}+z^{3}=n}$ est donnée par les valeurs correspondantes, soit :

${\displaystyle (-2901096694)^{3}+(-15550555555)^{3}+15584139827^{3}=24}$.

Intérêt public

Le problème des sommes de trois cubes a été popularisé aux États-Unis par Brady Haran, créateur de la chaîne Numberphile sur YouTube ; avec en 2015 une vidéo intitulée « The Uncracked Problem with 33 » contenant une interview de Timothy Browning ; six mois plus tard une autre vidéo avec Browning, intitulée « 74 is Cracked », parle de la découverte par Huisman en 2016 d'une solution pour 74. En 2019, Numberphile publie trois vidéos intitulées « 42 is the new 33 », « The mystery of 42 is solved » et « 3 as the sum of 3 cubes », pour signaler la découverte de solutions pour 33, 42, et la nouvelle solution pour 3^,,.

La solution de Booker pour 33 a été décrite aux États-Unis dans des articles de Quanta Magazine et New Scientist, ainsi que dans Newsweek qui annonce la collaboration de Booker et Sutherland en ces termes : « ...the mathematician is now working with Andrew Sutherland of MIT in an attempt to find the solution for the final unsolved number below a hundred: 42. ». En France, un article en parle dans Pour la Science, un autre dans les Images des mathématiques.

Le nombre 42 a suscite un intérêt supplémentaire à cause de son apparition dans le roman de science-fiction Le Guide du voyageur galactique de Douglas Adams où il est la réponse à « la grande question sur la vie, l'univers et le reste ».

L'annonce de la solution pour 42 par Booker et Sutherland^, a eu un écho international, y compris un article dans New Scientist, The Daily Mail, Die Zeit, Der Spiegel, et aussi sur Futura Science, Gurumed, Hitek ou Tangente.

Solvabilité et décidabilité

En 1992, Roger Heath-Brown a conjecturé que tout entier ${\displaystyle n}$ qui n'est pas congru à 4 ou 5 modulo 9 possède une infinité de représentations comme somme de trois cubes. Le cas ${\displaystyle n=33}$ de ce problème a été utilisé par Bjorn Poonen comme premier exemple illustrant un article de synthèse sur les problèmes indécidables en théorie des nombres, dont le dixième problème de Hilbert est l'exemple le plus connu. Même si ce cas particulier a été résolu depuis, il n'est pas connu si le problème de représenter un entier comme somme de trois cubes est décidable.

Si la conjecture de Heath-Brown est vraie, le problème est décidable. Dans ce cas, un algorithme consiste simplement à calculer le reste de ${\displaystyle n}$ modulo 9, et de retourner « non » si la valeur est 4 ou 5, et « oui » sinon. L'article de Heath-Brown contient aussi des conjectures sur la limite des entiers à tester pour trouver une solution explicite.

Variantes

• Une variante du problème liée au problème de Waring est la question de la représentation comme somme de trois cubes d'entiers naturels. Au XIX^e siècle, Charles Gustave Jacob Jacobi et ses collaborateurs ont compilé des tables de solutions pour ce problème. Il est conjecturé que les nombres représentables ont une densité positive^,. La question reste ouverte, mais Trevor Wooley a montré que ${\displaystyle \Omega (n^{0.917})}$ de ces nombres entre ${\displaystyle 1}$ et ${\displaystyle n}$ possèdent de telles représentations^,,. La densité est au plus ${\displaystyle \Gamma (4/3)^{3}/6\approx 0,119}$.

• Tout entier peut être représenté comme somme de trois cubes de nombres rationnels (plutôt que comme somme de cubes d'entiers)^,.Cette propriété a déjà été démontrée en 1825 dans le Ladies' Diary n° 35 par un certain S. Ryley qui a fourni la famille de solution (non exhaustive) pour ${\displaystyle x^{3}+y^{3}+z^{3}=k}$ :
  • ${\displaystyle x={\frac {(9d^{6}-30k^{2}d^{3}+k^{4})(3d^{3}+k^{2})+72k^{4}d^{3}}{6kd(3d^{3}+k^{2})^{2}}},y={\frac {30k^{2}d^{3}-9d^{6}-k^{4}}{6kd(3d^{3}+k^{2})}},z={\frac {18kd^{5}-6k3d^{2}}{(3d^{3}+k^{2})^{2}}}}$.
  • Par exemple, ${\displaystyle 4=\left({\frac {5}{3}}\right)^{3}+\left(-{\frac {6}{7}}\right)^{3}+\left({\frac {1}{3\times 7}}\right)^{3}=\left({\frac {1}{3}}\right)^{3}+\left({\frac {30}{19}}\right)^{3}+\left({\frac {17}{3\times 19}}\right)^{3}}$.

Notes et références

Liens externes

• Hisanori Mishima, « Solutions of n = x³ + y³ + z³ for 0 ≤ n ≤ 99 »
• Daniel J. Bernstein, « threecubes »,
• Mathpages, « Sums of three cubes »
• Timothy Browning, « The Uncracked Problem with 33 », sur Numberphile
• Timothy Browning, « 74 is cracked », sur Numberphile
• Andrew Booker, « 42 is the new 33 », sur Numberphile
• Andrew Booker, « The Mystery of 42 is Solved », sur Numberphile
• Andrew Booker, « 3 as a sum of 3 cubes », sur Numberphile

Articles liés

• Problème des quatre cubes
• Problème de Waring

• Arithmétique et théorie des nombres

1. 42 (nombre)
2. 73 (nombre)
3. Théorème des trois carrés
4. Problème de Waring
5. Conjecture d'Euler
6. Problème des quatre cubes
7. Y (Somme)
8. Tesseract
9. Seine-Saint-Denis
10. Somme de contrôle
11. Charity Engine
12. Nombre triangulaire
13. Groupe du Rubik's Cube
14. Racine carrée de trois
15. Black Cube
16. Hellraiser
17. Histoire de la plomberie
18. Solide de Platon
19. Géographie de la France
20. Cube Soma