在数学中，傅里叶级数（英語：Fourier series，/ˈfʊrieɪ, -iər/）是把类似波的函数表示成简单谐波的方式。更正式地说，对于满足狄利克雷定理的周期函数，其傅里叶级数是由一组正弦与余弦函数的加权和表示的方法。傅里叶级数与用来找出无周期函数的频率信息的傅里叶变换有密切的关系。

傅里叶级数是傅里叶分析的一个研究分支，也是采样定理原始证明的核心。傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。

歷史

傅里叶级数得名于法国数学家约瑟夫·傅里叶（1768年–1830年），他提出任何函数都可以展开为三角级数。此前数学家欧拉、达朗贝尔和克莱罗，已发现在认定一個函数有三角级数展开后，通过积分方法计算其系数的公式，而拉格朗日等人已经找到了一些非周期函数的三角级数展开。将周期函数分解为简单振荡函数的总和的最早想法，可以追溯至公元前3世紀古代天文學家的均輪和本輪學說。

傅里叶的工作得到了丹尼尔·伯努利的赞助，傅里叶介入三角级数用來解热传导方程，其最初论文雖經西尔维斯特·拉克鲁瓦、加斯帕尔·蒙日同意，但在1807年经拉格朗日、拉普拉斯和勒讓德评審后被拒绝出版，他的现在被称为傅里葉逆轉定理的理论后来发表于1822年出版的《热的解析理论》。

定義

傅里叶级数可以用不同的形式来表达，下面将周期为${\displaystyle P}$的一个周期函數${\textstyle s(x),\ x\in \mathbb {R} }$表达为不同形式的傅里叶级数。

正弦-余弦形式

人们常用${\displaystyle \sin(x)}$與${\displaystyle \cos(x)}$的三角級數來表示${\textstyle s(x)}$，就是将所有${\displaystyle n}$階諧波${\textstyle \sin({\frac {2\pi nx}{P}})}$與${\textstyle \cos({\frac {2\pi nx}{P}})}$，乘以其各自在${\textstyle s(x)}$中的權重，求得它们的總和；这些${\displaystyle n}$階諧波的權重稱爲傅立葉級數係數，它们可以藉由如下積分來獲得：

符号${\textstyle \int _{P}}$表示在选定区间上的积分，典型的选择为${\displaystyle [-P/2,P/2]}$或者${\displaystyle [0,P]}$。注意${\displaystyle A_{0}}$是函数${\displaystyle s(x)}$的平均值，这个性质扩展到了类似的变换比如傅里叶变换。

通过这些系数定义傅里叶级数为：

这里使用符号${\displaystyle \sim }$，表示傅里叶级数的求和不一定总是等于${\displaystyle s(x)}$。普遍來說${\displaystyle n}$是理論上趨近於無限大的，但是就算趨近於無限大，對所有的${\displaystyle x}$（例如在某一點上不連續），傅立葉級數也不一定收斂到${\textstyle s(x)}$ 。尽管不收斂的可能性始终存在，在科学和工程领域中经常将Eq. 2中的${\displaystyle \sim }$直接替代为${\displaystyle =}$。

在傅里叶级数系数中的整数索引${\displaystyle n}$，是级数中相应的${\displaystyle \cos }$或${\displaystyle \sin }$，在这个函数的周期${\displaystyle P}$中，形成的圆周（cycle）的数目。因此对应于${\displaystyle A_{n}}$和${\displaystyle B_{n}}$的项有着：

• 波长等于${\displaystyle {\tfrac {P}{n}}}$，并且有着同于${\displaystyle x}$的单位。
• 频率等于${\displaystyle {\tfrac {n}{P}}}$，并且有着${\displaystyle x}$的倒数单位。

指数形式

下面藉由歐拉公式${\displaystyle \ e^{ix}=\cos x+i\sin x\ }$，将傅里叶级数系数简化成复数指數形式。

根據定義，我們可以得到:

通过将等式Eq. 1代入Eq. 3，可以证实：

给定复数傅里叶级数系数，可以用公式复原出${\displaystyle A_{n}}$和${\displaystyle B_{n}}$：

通过这些定义，傅里叶级数可以写为：

这是可推广到复数值域函数的惯用形式。${\displaystyle n}$的负数值对应于负频率。

複數值函數

人们習慣將${\textstyle s(x)}$的值域普遍化到複數上，设${\textstyle s(x)}$是一個複數值函數，它的實部和虛部，都是實數值函數：

${\displaystyle s(x)=\operatorname {Re} (s(x))+i\cdot \operatorname {Im} (s(x)),\quad x\in \mathbb {R} }$

定义${\displaystyle c_{n}\triangleq c_{_{Rn}}+i\cdot c_{_{In}}}$则：

${\displaystyle c_{n}={\frac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx={\frac {1}{P}}\int _{P}\operatorname {Re} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx+i\cdot {\frac {1}{P}}\int _{P}\operatorname {Im} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}$

${\displaystyle c_{_{Rn}}={\frac {1}{P}}\int _{P}\operatorname {Re} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}$

${\displaystyle c_{_{In}}={\frac {1}{P}}\int _{P}\operatorname {Im} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}$

对于这个复数值函数，它的傅里叶级数的实部，是它的实部的傅里叶级数；它的傅里叶级数的虚部，是它的虚部的傅里叶级数：

${\displaystyle s(x)\sim \sum _{n=-\infty }^{\infty }\left(c_{_{Rn}}+i\cdot c_{_{In}}\right)\cdot e^{i{\tfrac {2\pi }{p}}nx}=\sum _{n=\infty }^{\infty }c_{_{Rn}}\cdot e^{i{\tfrac {2\pi }{p}}nx}+i\cdot \sum _{n=-\infty }^{\infty }c_{_{In}}\cdot e^{i{\tfrac {2\pi }{p}}nx}}$

振幅-相位形式

還可以利用三角恆等式${\displaystyle \ \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta \,}$，把正弦-余弦形式中後面的正弦函數跟餘弦函數合併起來：

${\displaystyle A_{n}\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)\ \equiv \ \underbrace {A_{n}\cos(\varphi _{n})} _{a_{n}}\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)+\underbrace {A_{n}\sin(\varphi _{n})} _{b_{n}}\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)}$

然後定義振幅${\textstyle A_{n}\triangleq {\sqrt {a_{n}^{2}+b_{n}^{2}}}}$，相位${\textstyle \varphi _{n}\triangleq \operatorname {arctan2} (b_{n},a_{n})}$，这里的${\displaystyle a_{n}}$和${\displaystyle b_{n}}$对应正弦-余弦形式中${\displaystyle A_{n}}$和${\displaystyle B_{n}}$。${\displaystyle {\tfrac {A_{0}}{2}}}$是${\displaystyle s(x)}$的平均值${\textstyle {\frac {1}{P}}\int _{P}s(x)\,dx}$。

部份求和算子

在描述傅里叶级数行为的时候，经常会为一个函数${\displaystyle f(x)}$介入部份求和算子${\displaystyle S_{N}}$：

这里的${\displaystyle c_{n}}$是${\displaystyle f}$的傅里叶系数。不同于微积分中的级数，傅里叶级数的部份求和必须采用对称形式，否则收敛结果可能不成立。

假設${\displaystyle f(x)}$與${\displaystyle g(x)}$是在${\textstyle \mathbb {R} }$上的可積函數，${\displaystyle f(x)}$與${\displaystyle g(x)}$在${\displaystyle [-\pi ,\pi ]}$的捲積${\displaystyle (f*g)(x)}$為:

${\displaystyle (f*g)(x)=\int _{-\pi }^{\pi }f(\tau )g(x-\tau )d\tau }$

周期为${\displaystyle 2\pi }$的函數${\displaystyle f(x)}$的傅立葉級數的部份求和，可以经由${\displaystyle f(x)}$与狄利克雷核${\textstyle D_{n}(x)=\sum _{k=-n}^{n}e^{ikx}}$的摺積来表示：

${\displaystyle {\begin{aligned}S_{N}(f)(x)&=\sum _{n=-N}^{N}c_{n}e^{inx}\\&=\sum _{n=-N}^{N}\left({\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(\tau )e^{-in\tau }d\tau \right)\cdot e^{inx}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(\tau )\left(\sum _{n=-N}^{N}e^{in(x-\tau )}\right)d\tau \\&={\frac {1}{2\pi }}(f*D_{N})(x)\end{aligned}}}$

收敛性概要

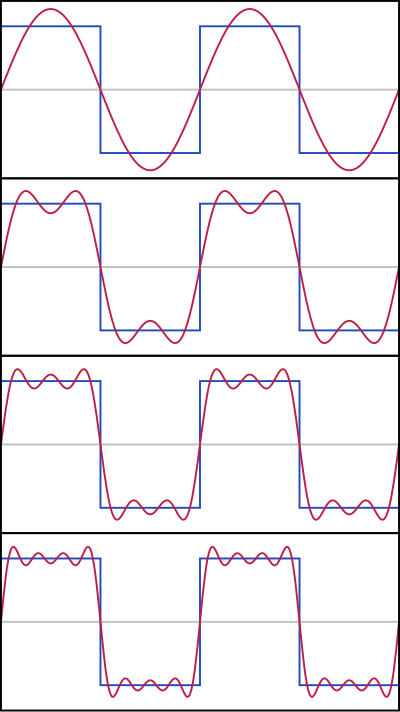
${\displaystyle s_{N}(x)}$在${\displaystyle [x_{0},\ x_{0}+P]}$近似了${\displaystyle s(x)}$，该近似程度会随着${\displaystyle N\rightarrow \infty }$逐渐改善。这个无穷和${\displaystyle s_{\infty }(x)}$叫做 ${\displaystyle s}$的傅里叶级数表示。傅里叶级数的收敛性取决于函数有限数量的极大值和极小值，这就是通常称为傅里叶级数的狄利克雷条件。参见傅里叶级数的收敛性之一。对于广义函数或分布也可以用范数或弱收敛定义傅里叶系数。在${\displaystyle s(x)}$的不可导点上，如果我们只取无穷级数中的有限项求和，那么在这些点上会有幅度不随${\displaystyle N}$增大而持续变小的起伏，这叫做吉布斯现象，一个简单的例子是方波信号。

在工程应用中，一般假定傅里叶级数除了在不连续点以外处处收敛，原因是工程上遇到的函数比数学家提供的这个假定的反例表现更加良好。特别地，傅里叶级数绝对收敛且一致收敛于${\displaystyle s(x)}$，只要在${\displaystyle s(x)}$的导数（或许不会处处存在）是平方可积的。如果一个函数在区间${\displaystyle [x_{0},x_{0}+P]}$上是平方可积的，那么此傅里叶级数在几乎处处的点都收敛于该函数。

其他常用表示法

符号${\displaystyle c_{n}}$在讨论多个不同函数的傅里叶系数时是不够用的。因此习惯上将其替代为函数（这里是函数${\displaystyle s}$）的某种修改形式，即采用函数式符号比如${\displaystyle {\hat {s}}[n]}$或${\displaystyle S[n]}$，来替代下标式符号：

${\displaystyle s(x)=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{2\pi inx/P}\quad }$常用的数学符号

${\displaystyle s(x)=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\quad }$常用的工程符号

在工程上，特别是在变量${\displaystyle x}$表示时间的时候，系数序列叫做频域表示。经常使用方括号来强调这个函数的定义域是频率的离散集合。

另一个常用频域表示，使用傅里叶级数系数，调制像梳子一样的狄拉克采样函数：

${\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)}$

这里的${\displaystyle f}$表示连续频域。在变量${\displaystyle x}$以秒为单位的时候，${\displaystyle f}$以赫兹为单位。采样的间隔为基本频率${\displaystyle {\tfrac {1}{P}}}$的${\displaystyle n}$倍（即为谐波）。 ${\displaystyle s_{\infty }(x)}$可以通过逆傅里叶变换从这种表示恢复出来:

${\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x)\end{aligned}}}$

构造出的函数${\displaystyle S(f)}$，因而通常称为“傅里叶变换”，即使一个周期函数的傅里叶积分在这个谐波频率上不收敛。

常用的傅里叶级数

下表列出常用的周期函数及其傅里叶级数系数。

• ${\displaystyle s(x)}$指示周期${\displaystyle P}$的周期函数。
• ${\displaystyle A_{0}}$、${\displaystyle A_{n}}$和${\displaystyle B_{n}}$指示周期函数${\displaystyle s(x)}$的傅里叶级数系数（正弦-余弦形式）。

基本性質

下表展示在时域中的一些数学运算及其对应的在傅里叶级数系数上的效果。

• 复数共轭指示为上标星号${\displaystyle \ ^{*}\ }$。
• ${\displaystyle s(x)}$和${\displaystyle r(x)}$指示周期为${\displaystyle P}$的函数或只定义在${\displaystyle x\in [0,P]}$中的函数。
• ${\displaystyle S[n]}$和${\displaystyle R[n]}$指示${\displaystyle s}$和${\displaystyle r}$的傅里叶级数系数（指数形式）。

对称性质

所有的函数都可以分解成唯一性的偶部和奇部：${\displaystyle f(x)=f_{\text{e}}(x)+f_{\text{o}}(x)}$，这里的${\textstyle f_{\text{e}}(x)={\frac {f(x)+f(-x)}{2}}}$而${\textstyle f_{\text{o}}(x)={\frac {f(x)-f(-x)}{2}}}$。实数参数的复数值函数${\displaystyle f:\mathbb {R} \to \mathbb {C} }$，对于所有${\displaystyle x\in \mathbb {R} }$，如果${\displaystyle f(x)={\overline {f(-x)}}}$则称其为“偶对称”，如果${\displaystyle f(x)=-{\overline {f(-x)}}}$则称其为“奇对称”，这里${\displaystyle {\overline {z}}}$的上顶横线指示复数共轭。

一个复数值函数的实部和虚部，分解成各自的偶部和奇部，就有了四个分量，分别用下标标明为RE、RO、IE和IO。一个复数值时间参数函数的四个分量，与它的复数频率变换的四个分量之间，有着一一映射：

${\displaystyle {\begin{array}{rccccccccc}{\text{时 域}}&s&=&s_{_{\text{RE}}}&+&s_{_{\text{RO}}}&+&i\ s_{_{\text{IE}}}&+&i\ s_{_{\text{IO}}}\\&{\Bigg \Updownarrow }{\mathcal {F}}&&{\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}\\{\text{频 域}}&S&=&S_{\text{RE}}&+&\,i\ S_{\text{IO}}\,&+&i\ S_{\text{IE}}&+&S_{\text{RO}}\end{array}}}$

由此可见，各种关系是显而易见的，例如：

• 实数值函数s_RE + s_RO的变换，是偶对称函数S_RE + i S_IO。反过来说，偶对称变换蕴含了实数值时域。
• 虚数值函数i s_IE + i s_IO的变换，是奇对称函数S_RO + i S_IE，反过来说也成立。
• 偶对称函数s_RE + i s_IO的变换，是实数值函数S_RE + S_RO，反过来说也成立。
• 奇对称函数s_RO + i s_IE的变换，是虚数值函数i S_IE + i S_IO，反过来说也成立。

範例

一个简单的傅里叶级数

我们现在用上面的公式给出一个简单函数的傅里叶级数展开式。考虑一个锯齿波：

${\displaystyle s(x)={\frac {x}{\pi }},\quad \mathrm {for} -\pi <x<\pi }$

${\displaystyle s(x+2\pi k)=s(x),\quad \mathrm {for} -\infty <x<\infty {\text{ and }}k\in \mathbb {Z} }$

在这种情况下，傅里叶级数为：

${\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1\end{aligned}}}$

可以证明，当${\displaystyle s}$可微时，傅立叶级数在每个点${\displaystyle x}$都收敛于${\displaystyle s(x)}$，于是：

当${\displaystyle x=\pi }$时，傅里叶级数收敛于${\displaystyle 0}$，为在${\displaystyle x=\pi }$ 处${\displaystyle s}$的左极限和右极限之和的一半。这是傅里叶级数的狄利克雷定理的特例。

这个例子为我们引出了巴塞尔问题的一种解法。

傅里叶诱导

在上例中我们的函数的傅里叶级数展开式看起来不比${\displaystyle s(x)={\tfrac {x}{\pi }}}$简单，因此人们需要傅里叶级数的原因也就不会立即显现出来。但还有很多应用，我们举用傅里叶诱导解热方程的例子。考虑边长为${\displaystyle \pi }$米的方形金属版，坐标为${\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}$。如果板内没有热源，并且四个边中三个都保持在${\displaystyle 0}$摄氏度，而第四条边${\displaystyle y=\pi }$，对于${\displaystyle x\in (0,\pi )}$，保持在温度梯度${\displaystyle T(x,\pi )=x}$摄氏度。在这种情况下，稳态（或者说很长时间过后的）热分布函数${\displaystyle T(x,y)}$不能得出解析解，但却可以证明：

${\displaystyle T(x,y)=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx){\sinh(ny) \over \sinh(n\pi )}}$

这里的${\displaystyle \sinh }$是双曲正弦函数。热方程的这个解是通过将${\displaystyle \pi s(x)}$的傅里叶级数的每一项乘以${\displaystyle {\tfrac {\sinh(ny)}{\sinh(n\pi )}}}$得到的。尽管示例的函数${\displaystyle s(x)}$的傅里叶级数似乎很复杂，用傅里叶的方法却可以求解这个热分布问题。

其他例子

我們也可以應用傅立葉級數去證明等周不等式，或是構造處處連續處處不可微的函數。

收斂性

至今还没有判断傅里叶级数的收敛性充分必要条件，但是对于实际问题中出现的函数，有很多种判别条件可用于判断收敛性。比如${\displaystyle x(t)}$的可微性或级数的一致收敛性。在闭区间上满足狄利克雷条件的函数表示成的傅里叶级数都收敛。狄利克雷条件如下：

1. 在定义区间上，${\displaystyle x(t)}$须绝对可积；
2. 在任一有限区间中，${\displaystyle x(t)}$只能取有限个极值点；
3. 在任何有限区间上，${\displaystyle x(t)}$只能有有限个第一类间断点。

满足以上条件的${\displaystyle x(t)}$傅里叶级数都收敛，且：

1.当${\displaystyle t}$是${\displaystyle x(t)}$的连续点时，级数收敛于${\displaystyle x(t)}$；

2.当${\displaystyle t}$是${\displaystyle x(t)}$的间断点时，级数收敛于${\displaystyle {\frac {1}{2}}[x(t^{-})+x(t^{+})]}$。

1966年，里纳特·卡尔松证明了勒贝格二次可积函数的傅立叶级数一定是几乎处处收敛的，即级数在除了一个勒贝格零测集外均收敛。

傅立葉級數收斂证明

假設一個函數在${\displaystyle f(x)}$在${\displaystyle [0,2\pi ]}$上是平方可積，則會有:

${\displaystyle {\frac {1}{2\pi }}\int _{0}^{2\pi }|f(x)-S_{N}(f)(x)|^{2}dx\rightarrow 0}$ 當${\displaystyle N\rightarrow \infty }$

證明的第一步:

考慮一系列正交基底，${\displaystyle \{e_{n}\}_{n\in \mathbb {Z} }}$，其中${\displaystyle e_{n}(x)=e^{-inx}}$，且有

${\displaystyle (e_{n},e_{m})={\begin{cases}1,&{\text{if }}n=m\\0,&{\text{if }}n\neq m\end{cases}}}$

然後有${\displaystyle (f,e_{n})={\frac {1}{2\pi }}\int _{0}^{2\pi }f(x)e^{-inx}dx={\hat {f}}(n)}$

特別的有，${\displaystyle f(x)}$的傅立葉級數的部分和${\displaystyle S_{N}(f)(x)=\sum _{|n|\leq N}{\hat {f}}(n)e_{n}}$

然後根據${\displaystyle f=f-\sum _{|n|\leq N}{\hat {f}}(n)e_{n}+\sum _{|n|\leq N}{\hat {f}}(n)e_{n}}$ 以及畢氏定理，可以有:

${\displaystyle ||f||^{2}=||f-\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}+||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}}$ 替換一下後有 ${\displaystyle ||f||^{2}=||f-S_{N}(f)(x)||^{2}+||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}}$

如果右邊第一項收斂到0，再根據正交的性質，可以看出上述式子中的右手邊第二項:

${\displaystyle ||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}=\sum _{|n|\leq N}|{\hat {f}}(n)|^{2}}$，這就證明了帕塞瓦尔定理。

证明的第二步:

回到證明右邊第一項，因為函數${\displaystyle f(x)}$可積，找到一個連續函數${\displaystyle g(x)}$，然後根據最佳逼近引理，可以找到一個三角多項式p(x)，使得

${\displaystyle |f-S_{N}(f)(x)|\leq |f(x)-g(x)|+|g(x)-S_{N}(f)(x)|}$

故當${\displaystyle N\rightarrow \infty }$，函數${\displaystyle f(x)}$跟${\displaystyle S_{N}(f)(x)}$的差為0。

其他性质

傅立葉級數的唯一性

如果有一個定義在${\displaystyle [-\pi ,\pi ]}$的函數${\displaystyle f(x)}$和${\displaystyle g(x)}$,其中函數${\displaystyle f(x)}$和${\displaystyle g(x)}$的傅立葉係數${\displaystyle {\hat {f}}(n)}$還有${\displaystyle {\hat {g}}(n)}$相同，且傅立葉級數都收斂到函數本身，那麼可以證明此傅立葉級數具有唯一性，也就是${\displaystyle f(x)=g(x)}$。換句話說，如果函數${\displaystyle f(x)}$在${\displaystyle [-\pi ,\pi ]}$上可積，傅立葉係數${\displaystyle {\hat {f}}(n)}$為0，對所有的${\displaystyle n\in \mathbb {N} }$，那麼函數${\displaystyle f(x)=0}$

卷积定理

给定周期为${\displaystyle P}$的函数${\displaystyle s_{_{P}}}$和${\displaystyle r_{_{P}}}$，它们具有傅里叶级数系数${\displaystyle S[n]}$和${\displaystyle R[n]}$，这里的${\displaystyle n\in \mathbb {Z} }$。

• 逐点乘积${\displaystyle h_{_{P}}(x)\triangleq s_{_{P}}(x)\cdot r_{_{P}}(x)}$，也是周期为${\displaystyle P}$，并且它的傅里叶级数系数是序列${\displaystyle S}$和${\displaystyle R}$的离散卷积：${\displaystyle H[n]=(S*R)[n]}$。
• 周期卷积${\textstyle h_{_{P}}(x)\triangleq (s_{_{P}}*r)(x)=(s*r_{_{P}})(x)=\int _{P}s_{_{P}}(\tau )\cdot r_{_{P}}(x-\tau )\,d\tau }$，也是周期为${\displaystyle P}$，它具有傅里叶级数系数：${\displaystyle H[n]=P\cdot S[n]\cdot R[n]}$。
• 在${\displaystyle c_{0}(\mathbb {Z} )}$中的双无限序列${\displaystyle \left\{c_{n}\right\}_{n\in Z}}$，是在${\displaystyle L^{1}([0,2\pi ])}$中的傅里叶系数的序列，当且仅当它是在${\displaystyle \ell ^{2}(\mathbb {Z} )}$中的两个序列的卷积。

微分性質

我們說${\displaystyle f(x)}$屬於在${\displaystyle C^{k}(\mathbb {T} )}$ ${\displaystyle \Rightarrow }$ 如果${\displaystyle f(x)}$是一個在實數上以${\displaystyle 2\pi }$為週期的函數，且${\displaystyle k}$次可微而且${\displaystyle k}$階連續。

• 如果${\displaystyle f(x)}$屬於在${\displaystyle C^{1}(\mathbb {T} )}$，那麼${\displaystyle f'(x)}$傅立葉係數${\displaystyle {\hat {f'}}(n)}$可以被用${\displaystyle f(x)}$傅立葉係數${\displaystyle {\hat {f}}(n)}$的表示，藉由公式${\displaystyle {\hat {f'}}(n)=in{\hat {f}}(n)}$

• 如果${\displaystyle f(x)}$屬於在${\displaystyle C^{k}(\mathbb {T} )}$，${\displaystyle {\hat {f^{(k)}}}(n)=(in)^{k}{\hat {f}}(n)}$。特別的，當固定${\displaystyle k\geq 1}$，我們有${\displaystyle {\hat {f^{(k)}}}(n)}$趨近於0當${\displaystyle n\rightarrow \infty }$，且有${\displaystyle {\hat {f^{(k)}}}(n)=O(1/n^{k})}$。

黎曼-勒贝格定理

如果${\displaystyle S}$是可积函数，则${\textstyle \lim _{|n|\to \infty }S[n]=0}$，${\textstyle \lim _{n\to +\infty }a_{n}=0}$而${\textstyle \lim _{n\to +\infty }b_{n}=0}$。

帕塞瓦尔定理

如果函數${\displaystyle f(x)}$屬於在${\displaystyle L^{2}([-\pi ,\pi ])}$之中，那麼便有${\textstyle \sum _{-\infty }^{\infty }|{\hat {f}}(n)|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}dx=||f||}$。

普朗歇爾定理

如果${\displaystyle c_{0},\,c_{\pm 1},\,c_{\pm 2},\ldots }$是系数，并且${\textstyle \sum _{n=-\infty }^{\infty }|c_{n}|^{2}<\infty }$，则有一个唯一的函数${\displaystyle s\in L^{2}(P)}$使得对于所有${\displaystyle n}$有着${\displaystyle S[n]=c_{n}}$。

延伸

希尔伯特空间的解读

所谓的两个不同向量正交是指它们的内积为0，这也就意味着这两个向量之间没有任何相关性,例如，在三维欧氏空间中，互相垂直的向量之间是正交的。事实上，正交是垂直在数学上的一种抽象化和一般化。一组n个互相正交的向量必然是线性无关的，所以必然可以张成一个n维空间，也就是说，空间中的任何一个向量可以用它们来线性表出。

在希爾伯特空間釋義下，函數的集合{e_n = e^inx; n ∈ Z}是[−π, π]平方可積函數L²([−π, π])的正交基。這個空間實際上是一個希爾伯特空間，有著針對任何兩個的元素f和g的如下內積:

${\displaystyle \langle f,\,g\rangle \;{\stackrel {\mathrm {def} }{=}}\;{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x){\overline {g(x)}}\,dx.}$

三角函数族的正交性用公式表示出来就是：

${\displaystyle \int _{-\pi }^{\pi }\cos(mx)\,\cos(nx)\,dx=\pi \delta _{mn},\quad m,n\geq 1,\,}$

${\displaystyle \int _{-\pi }^{\pi }\sin(mx)\,\sin(nx)\,dx=\pi \delta _{mn},\quad m,n\geq 1}$

(這裡的δ_mn是克羅內克函數)，而

${\displaystyle \int _{-\pi }^{\pi }\cos(mx)\,\sin(nx)\,dx=0;\,}$

参阅

• 离散时间傅里叶级数
• 傅里叶变换
• 维尔斯特拉斯逼近定理

注释

引用

延伸阅读

外部链接

• Hazewinkel, Michiel (编), Fourier series, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
• Hobson, Ernest. Fourier's Series. Encyclopædia Britannica 10 (第11版). London: 753–758. 1911. 
• 埃里克·韦斯坦因. Fourier Series. MathWorld. 

本條目含有来自PlanetMath《example of Fourier series》的內容，版权遵守知识共享协议：署名-相同方式共享协议。

Articles connexes

1. 离散傅里叶级数
2. 傅里叶变换
3. 离散时间傅里叶变换
4. 离散傅里叶变换
5. 约瑟夫·傅里叶
6. 狄利克雷定理 (傅里叶级数)
7. 级数
8. 三角级数
9. 傅里叶分析
10. 级数展开
11. 微积分学教程
12. 洛朗级数
13. 调和级数
14. 狄利克雷核
15. 調和分析
16. 吉布斯现象
17. 傅立叶变换家族中的关系
18. 短時距傅立葉變換
19. 傅里叶 (消歧义)
20. DFS