Modelo de seis rayos

El modelo de seis rayos es un modelo aplicado a un entorno urbano o interior típico, donde una señal de radio transmitida desde una fuente fija encontrará varios objetos en el entorno que producen copias reflejadas, difractadas o dispersas de la señal transmitida, estas copias de la señal transmitidas son llamadas componentes de la señal de trayectos múltiples. La señal trasmitida LOS (línea de vista ) y las componentes de la señal de trayectos múltiples son sumadas en el receptor.

En este modelo de trazado de rayos se suponen un número infinito de reflectores con ubicación conocida que poseen propiedades dieléctricas. Este modelo se aproxima a la solución por las ecuaciones de Maxwell el cual no aplicamos por su complejidad es poco práctico; por lo tanto, los efectos de reflexión, difracción y dispersión en el frente de onda se aproximan usando simples ecuaciones geométricas en lugar de las ecuaciones de maxwell.

El error de la aproximación de trazado de rayos es menor cuando el receptor tiene muchas longitudes de onda del dispersor más cercano y todos los dispersores son grandes en relación con una longitud de onda.

El enfoque del modelo de dos rayos se puede ampliar fácilmente para añadir tantos rayos según sea necesario. Podemos agregar los rayos rebotan en cada lado de una calle en un corredor urbano, lo que lleva a un modelo de seis rayos.

Deducción matemática

Los efectos de la difracción, dispersión y reflexión del frente de la onda se aproxima usando ecuaciones geométricas que permite encontrar la longitud de cada rayo y a la vez la distancia ${\displaystyle d}$, teniendo en cuenta la altura del transmisor ${\displaystyle ht}$ y la altura del receptor ${\displaystyle hr}$,donde los factores que son importante para cualquier modelo de rayos como son: el rayo directo ${\displaystyle R0}$ y los reflejados ${\displaystyle R1}$ y ${\displaystyle R2}$ que nos dan: el coeficiente de reflexión, las ganancias de las antenas transmisora y receptora ${\displaystyle Gp}$, la potencia recibida ${\displaystyle Pr}$ y la velocidad de la onda.

Análisis para antenas de alturas iguales ubicadas en el centro de la calle.

Teniendo en cuenta que la altura no presenta variación en las antenas entonces ${\displaystyle h_{t}=h_{r}=h}$, por lo cual se determina que para los siguientes dos rayos que se reflejan en una ocasión en la pared, el punto en el cual chocan es igual a dicha altura ${\displaystyle h}$. Así mismo por cada rayo que se refleja en la pared existe otro rayo que se refleja en el suelo en un número igual a las reflexiones en la pared más uno, en dichos rayos existen distancias diagonales por cada reflexión y la sumatoria de dichas distancias es denominada ${\displaystyle d'}$ .

Al estar ubicadas en el centro de la calle la distancia entre las antenas ${\displaystyle T_{X}}$, ${\displaystyle R_{X}}$ y las edificaciones y el ancho de las calles son iguales en ambos lados por lo que ${\displaystyle w_{t1}=w_{r1}=w_{t2}=w_{r2}}$, definiendo así una sola distancia ${\displaystyle w}$.

El modelo matemático de propagación de seis rayos se basa en el modelo de dos rayos, para encontrar las ecuaciones de cada rayo involucrado. La distancia ${\displaystyle d}$ que separa las dos antenas, es igual al primer rayo directo ${\displaystyle R_{0}}$ o línea de vista (LOS), es decir:

${\displaystyle R_{0}=d}$

Para el rayo reflejado por debajo de este ${\displaystyle R_{0}}$ se aplica el teorema de Pitágoras, en el triángulo rectángulo que se forma entre la reflexión de ${\displaystyle R_{0}}$ como hipotenusa y el rayo directo obteniendo:

${\displaystyle R_{0}^{'}={\sqrt {d^{2}+(2*h)^{2}}}}$

Para ${\displaystyle R_{1}}$ se vuelve a aplicar el teorema de Pitágoras, pero sabiendo que uno de los catetos es el doble de las distancias entre el transmisor y el edificio debido a la reflexión de ${\displaystyle w}$ y la distancia diagonal a la pared:

${\displaystyle R_{1}={\sqrt {d^{2}+(2*w)^{2}}}}$

Para ${\displaystyle R_{1}}$ se multiplica dos veces el segundo rayo pero se tiene en cuenta que la distancia es la mitad de la distancia del tercer rayo para formar el triángulo equivalente teniendo en cuenta que ${\displaystyle d_{1}}$ es el la mitad de la distancia de ${\displaystyle R_{1}}$debe ser la mitad de la distancia de línea de vista ${\displaystyle d}$:

${\displaystyle R_{1}^{'}=2*{\sqrt {\left({\frac {R_{1}}{2}}\right)^{2}+(2h)^{2}}}}$

Para ${\displaystyle R_{1}}$ y ${\displaystyle R_{2}}$ la deducción y las distancias son iguales por lo tanto:

${\displaystyle R_{2}=R_{1}}$

${\displaystyle R_{2}^{'}=R_{1}^{'}}$

Análisis para antenas de alturas iguales ubicadas en cualquier punto de la calle

Debido a que el rayo directo LOS no varía y no se presenta variación angular entre los rayos, la distancia de los dos primeros rayos ${\displaystyle R_{0}}$ y ${\displaystyle R_{0}^{'}}$ del modelo no varían y se deducen según el modelo matemático para dos rayos.^[1]​ Para los cuatro rayos restantes se aplica el siguiente procedimiento matemático:

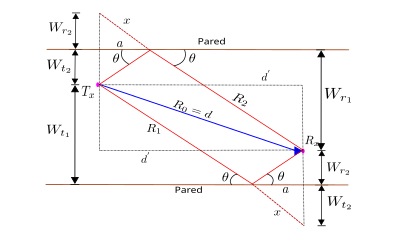
${\displaystyle R_{1}}$ Se obtiene la siguiente a través del análisis geométrico de la vista superior del modelo y aplicando el teorema de Pitágoras en los triángulos, teniendo en cuenta que las distancias entre la pared y las antenas ${\displaystyle w_{t1}}$, ${\displaystyle w_{r1}}$, ${\displaystyle w_{t2}}$, ${\displaystyle w_{r2}}$ son distintas:

${\displaystyle d^{'}={\sqrt {d^{2}-(w_{t1}-w_{r2})^{2}}}}$

Por semejanzas de triángulos en la vista superior del modelo se determina la ecuación de ${\displaystyle R_{1}}$:

${\displaystyle R_{1}={\sqrt {(d^{'})^{2}+(w_{t1}+w_{t2}-w_{r2})^{2}}}}$

${\displaystyle x={\frac {(w_{r2}*R_{1})}{w_{r2}+w_{t2}+w_{t1}-w_{r2}}}}$

${\displaystyle R_{1}^{'}={\sqrt {(R_{1}-x)^{2}+(2*h)^{2}}}+{\sqrt {(x)^{2}+(2*h)^{2}}}}$

Para ${\displaystyle R_{1}}$ y ${\displaystyle R_{2}}$ la deducción y las distancias son iguales por lo tanto:

${\displaystyle R_{2}=R_{1}}$

${\displaystyle R_{2}^{'}=R_{1}^{'}}$

Análisis para antenas de alturas diferentes ubicadas en la mitad de la calle.

Para antenas de diferentes alturas con rayos que rebotan en la pared, se observa que la pared es el punto medio donde los dos rayos transmitidos caen sobre dicha pared. Esta pared tiene una altura media entre las alturas del ${\displaystyle T_{X}}$ y el ${\displaystyle R_{X}}$ _. Es decir más pequeña que el del transmisor y más alta que el receptor y esta altura es donde los dos rayos impactan en este punto, luego rebotan hacia el receptor. El rayo reflejado deja dos reflexiones, una que posee la misma altura de la pared y otra la del receptor, y el rayo de línea de vista mantiene su misma dirección entre el ${\displaystyle T_{X}}$ y el ${\displaystyle R_{X}}$ _. La distancia diagonal ${\displaystyle d'}$ que separa las dos antenas se divide en dos distancias por medio de la pared una se denomina ${\displaystyle a}$ y otra la ${\displaystyle d-a}$.^[2]​

Para el modelo matemático de la propagación de seis rayos para antenas de alturas diferentes ubicadas en la mitad de la calle, Para el modelo matemático de la propagación de seis rayos para antenas de alturas diferentes ubicadas en cualquier punto de la calle, cada antena tiene una altura diferente, entonces ${\displaystyle h_{t}\neq h_{r}}$, hay una distancia directa ${\displaystyle d}$ que separa las dos antenas, el primer rayo se forma aplicando teorema de Pitágoras desde la diferencia de alturas de las antenas con respecto a la línea de vista:

${\displaystyle R_{0}={\sqrt {(d)^{2}+(h_{t}-h_{r})^{2}}}}$

El segundo rayo o el rayo reflejado se hace similar el primer rayo pero se suma las alturas de las antenas para formar el triángulo rectángulo por la reflexión de la altura del transmisor:

${\displaystyle R_{0}^{'}={\sqrt {(d)^{2}+(h_{t}+h_{r})^{2}}}}$

Para deducir el tercer rayo se halla el ángulo entre la distancia directa ${\displaystyle d}$ y la distancia de Línea de mira |línea de vista ${\displaystyle R_{0}}$

${\displaystyle \cos \theta ={\frac {h_{t}-h_{r}}{R_{0}}}}$

Ahora sabiendo que la distancia de las 2 antenas en la pared es ${\displaystyle d'}$ entonces la distancia en la que chocan los rayos equivale a ${\displaystyle \left({\frac {d'}{2}}\right)}$ y ahora se deduce la altura que resta de la pared con respecto a la altura del receptor llamado ${\displaystyle z}$ por semejanza de triángulos:

${\displaystyle {\frac {z}{a}}={\frac {h_{t}}{d^{'}}}}$

${\displaystyle z={\frac {h_{t}*~a}{d^{'}}}}$

Por semejanzas de triángulos se puede deducir la distancia donde choca el rayo a la pared hasta la perpendicular de receptor obteniendo:

${\displaystyle {\frac {a}{w^{t2}}}={\frac {d^{'}}{w_{t1}+w_{r1}}}}$

${\displaystyle a={\frac {d^{'}*w_{t2}}{\left(w_{t1}+w_{r1}\right)}}}$

${\displaystyle R_{1}={\frac {{\sqrt {(h_{t}-h_{r}-z)^{2}+({\frac {d'}{2}})^{2}}}+{\sqrt {z^{2}+a^{2}}}}{\cos \theta }}}$

Por semejanzas de triángulos se deduce la ecuación del cuarto rayo observando la:

${\displaystyle R_{1}^{'}={\frac {{\sqrt {(h_{t}+h_{r}+z)^{2}+({\frac {d'}{2}})^{2}}}+{\sqrt {(2h_{r}+z)^{2}+a^{2}}}}{\cos \theta }}}$

Para ${\displaystyle R_{1}}$ y ${\displaystyle R_{2}}$ la deducción y las distancias son iguales por lo tanto:

${\displaystyle R_{2}=R_{1}}$

${\displaystyle R_{2}^{'}=R_{1}^{'}}$

Análisis para antenas de alturas diferentes ubicadas en cualquier punto de la calle.

Para el modelo matemático de la propagación de seis rayos para antenas de alturas diferentes ubicadas en cualquier punto de la calle, cada antena tiene una altura diferente, entonces ${\displaystyle h_{t}\neq h_{r}}$, hay una distancia directa ${\displaystyle d}$ que separa las dos antenas igual que en caso anterior por esto se puede utilizar ${\displaystyle R_{0}}$ y ${\displaystyle R'_{0}}$ del caso anterior.

Ahora se deduce la altura que resta de la pared se puede hallar del mismo modo debido a que ahora la distancia en la que choca ya no sería ${\displaystyle \left({\frac {d'}{2}}\right)}$ ya que el choque no es en la mitad de la pared en lugar de esto sería ${\displaystyle d'-a}$.

Por semejanzas de triángulos se puede deducir la distancia donde choca el rayo a la pared hasta la perpendicular de receptor obteniendo:

${\displaystyle R_{1}={\frac {{\sqrt {(h_{t}-h_{r}-z)^{2}+(d^{'}-a)^{2}}}+{\sqrt {z^{2}+a^{2}}}}{\cos \theta }}}$

Por semejanzas de triángulos se deduce la ecuación del cuarto rayo observando la:

${\displaystyle R_{1}^{'}={\frac {{\sqrt {(h_{t}+h_{r}+z)^{2}+(d^{'}-a)^{2}}}+{\sqrt {(2h_{r}+z)^{2}+a^{2}}}}{\cos \theta }}}$

Para ${\displaystyle R_{1}}$ y ${\displaystyle R_{2}}$ la deducción y las distancias son iguales por lo tanto:

${\displaystyle R_{2}=R_{1}}$

${\displaystyle R_{2}^{'}=R_{1}^{'}}$

Perdidas por trayectoria de espacio libre

Se considera una señal transmitida a través del espacio libre a un receptor situado a una distancia d del transmisor. Asumiendo que no hay obstáculos entre el transmisor y el receptor, la señal se propaga a lo largo de una línea recta entre las dos. El modelo de rayo asociado con esta transmisión se llama Línea de mira |línea de vista (LOS), y la señal recibida correspondiente se llama señal de LOS.^[3]​

Para simplificar el modelo supondremos que ${\displaystyle T}$ es pequeña comparada con la longitud del código de la información útil, es decir, ${\displaystyle s(t)=s(t-T)}$ para un rebote fuera de la tierra, esa suposición es bastante segura, pero en general tendrá que recordar que tal suposición significa que se supone que la dispersión de retardo (difusión de los valores de ${\displaystyle T}$) es pequeña en comparación con las velocidades de símbolo de transmisión.

La pérdida de trayectoria por espacio libre del modelo de seis rayos en el espacio libre está definida como:

${\displaystyle p_{0}(t)={\sqrt {(G_{i}G_{r})}}{\frac {\lambda }{4\pi }}\left({\frac {\exp(j*2\pi *R_{0}/{\lambda })}{R_{0}}}+\Gamma {\frac {\exp(j*2\pi *R_{0}^{'}/{\lambda })}{R_{0}^{'}}}\right)}$

${\displaystyle p_{1}(t)={\sqrt {(G_{i}G_{r})}}{\frac {\lambda }{4\pi }}~\Gamma _{1}\left({\frac {\exp(j*2\pi *R_{1}/{\lambda })}{R_{1}}}+\Gamma {\frac {\exp(j*2\pi *R_{1}^{'}/{\lambda })}{R_{1}^{'}}}\right)}$

${\displaystyle p_{2}(t)={\sqrt {(G_{i}G_{r})}}{\frac {\lambda }{4\pi }}~\Gamma _{1}\left({\frac {\exp(j*2\pi *R_{2}/{\lambda })}{R_{2}}}+\Gamma {\frac {\exp(j*2\pi *R_{2}^{'}/{\lambda })}{R_{2}^{'}}}\right)}$

${\displaystyle P_{l}~(dB)=20\log \left|~\sum _{i=0}^{N}P_{i}~\right|}$

${\displaystyle {\lambda }=}$ ${\displaystyle {c \over f}}$ longitud de onda.

${\displaystyle T=}$ diferencia de tiempo entre los dos caminos.

${\displaystyle \Gamma =}$ coeficiente de reflexión de tierra.

${\displaystyle G_{i}=}$ganancia del transmisor.

${\displaystyle G_{r}=}$ganancia del receptor.

Véase también

• Modelo de diez rayos
• Trazado de rayos

Referencias